sin cos tan（サイン コサイン タンジェント）って
大人になっても使うの？って論争がありますよね。
少し学校で習う三角関数とは違いますけど
金型では割と普通に使います。
今回は関数電卓で求めたい場合の例を挙げて行きます。
三角関数
使う内容としましては
中学レベルの数学です。
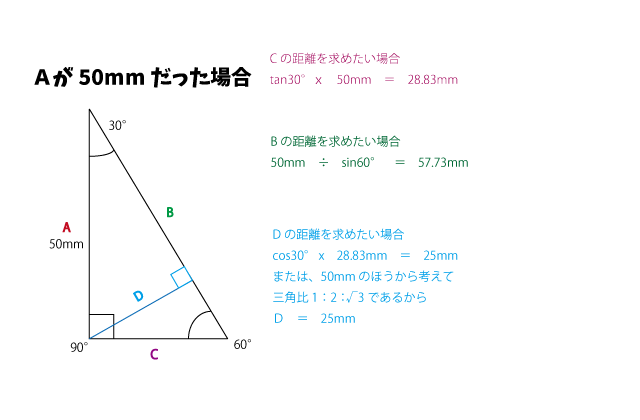
簡単なサンプルを作りました。 中学レベルの三角関数です。
斜辺、隣片、対辺（一番長い線、二番目に長い線、一番短い線）で
それぞれ分かっている数字（角度）から計算して
各々の数字を導き出していきます。
基本は直角三角形を作ることです！
金型での応用
特に勾配を付けた時の距離を調べる場合、
または修理で使うことが多くなります。
スライドにカシリがでて、再度合わせが必要になってくる場合や
バリ修理の場合に
元の寸法からどれだけ残せば強く当てることが
出来るかっていう時などに関数電卓を用いて計算します。
勾配の計算
まず、簡単な勾配の計算を先にやります。
使うのはtan（タンジェント）で
高さが100mmある製品の抜き勾配を計算する例です。
勾配を0.5°（30’）付けたい場合、
100 ｘ tan0.5 ＝0.8726 という答えがでます。
つまり、100mmの高さのある製品に0.5°の勾配をつけると
上から下まで0.8726の距離が出来ますよってことなんですね。
上のサンプル図でいうとＣの距離を求めていることと同じになります。
関数電卓で、0.5を押して、tanを押します。
すると0.008726～と数字が出てくるので、それに100をかけるっていう要領です。
勾配の計算はこれだけですので非常に簡単に求めることができます。
応用編
ここからはちょっとイメージの難しい例を紹介します。
もはやパターンですので、
こういう場合はこの計算って覚えてしまえば
なんてことはないです。あと関数電卓さえあれば！
例１
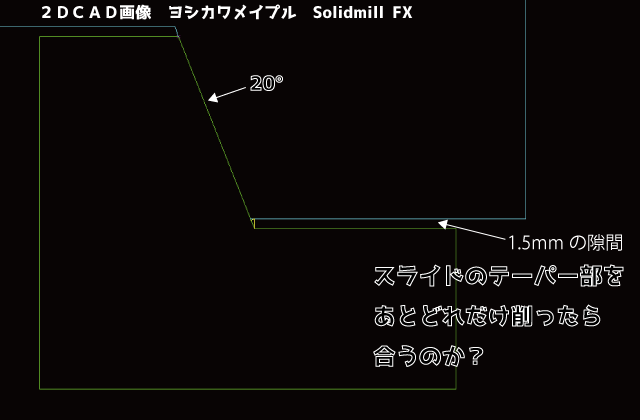
スライドあわせでＰＬ面に1.5mmの隙間ができてしまっています。 あとどれだけテーパー部分を削れば合ってくれるのか？
計算方法、考え方は次のようになります。
答えは0.513mmになります。
分かっている数字は1.5mmという隙間です。
あと角度が20°ということですね。
（すみません、図が28°みたいに見えるところがありますが、フォントの関係で本当は20°です）
Ａの対辺の数字が、削る寸法になりますので
sin20° ｘ 1.5 ＝ 0.513
Ａ＝0.513になります。
こういう場合はもう、
sin○°ｘＰＬスキマ距離 というパターンで
覚えてしまってＯＫです。
例２
次の例は
スライドバリ修正の場合の計算方法です。
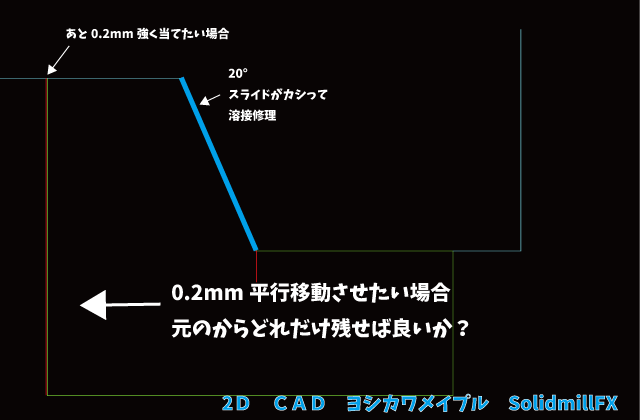
0.2mmのバリが出ているからあと0.2mm強く合わせたい。 とりあえず溶接してどれだけ残せば0.2mm強く合わせられるか？
もう、ぱっと見計算方法なんだけ？？？って
状態です。ＣＡＤとかせめて絵を描かないと・・・
そんなときの計算方法がこちらです。
0.188が答えです。ほぼ0.2mmじゃないか！？
分かっている数字は0.2mmとスライドテーパーの20°です。
Ａの値が分かれば残し量が出てきます。
この場合の関数電卓での計算方法は
cos20° ｘ 0.2mm ＝ 0.188
となります。ほぼ0.2mmでした・・・
あと○mm強く当てたい！っていうときの
関数電卓でのパターンは
cos○° ｘ 平行に動かしたい距離 になりますので
覚えておくとその場で計算出来ます。
まとめ
まだまだいろんな状況があるかと思いますが、
こういうのを覚えておけば、
図やＣＡＤをわざわざ描きにいったりしなくても
関数電卓さえあればその場で計算出来てしまいます。
斜辺がどうとか隣片ｘ対辺～とか難しく
考えずに、パターンで覚えてしまえばなんてことないので
こういう場合はこれっていう
パターンとして覚えてしまうと良いと思います。
ＰＬのスキマから計算する場合
sin○°ｘＰＬスキマ距離
あと○mm強く当てたい時の計算
cos○° ｘ 平行に動かしたい距離
あと、困ったことに関数電卓によっては
数字を先にいれるものとsin cos tanを先にいれるものと
ごっちゃになっています。
こういうのは統一して欲しいですよね。
関連記事としてこちらもどうぞ
